L’addizione e la sottrazione sono due operazioni chiamate operazioni inverse, cioè per “tornare indietro” dopo aver fatto una addizione bisogna fare una sottrazione e viceversa, detto questo vediamo la tecnica per fare questo passaggio.

Sappiamo tutti fin dalle scuole elementari che la sottrazione viene definita nel seguente modo

   

e scritta nello schema generale possiamo dire che

   

Notiamo che con un disegno questo risulta particolarmente immediato

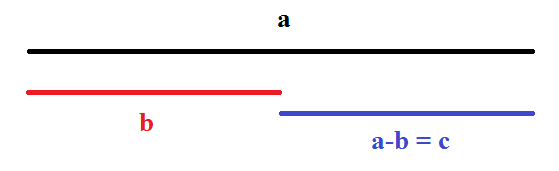
cioè se il segmento nero (a) meno il segmento rosso (b) è uguale al segmento blu (c) allora il segmento nero è uguale al segmento rosso più il segmento blu.

Questa proprietà si dimostra molto utile per risolvere i problemi del tipo:

Che numero deve stare al posto della se:
Che numero deve stare al posto della se:

Che numero deve stare al posto della se:
Che numero deve stare al posto della se:

Vediamo come affrontare questi problemi con questa relazione.

Caso 1/2

I primi due casi, e , sono esattamente lo stesso caso, questo a livello teorico segue dalla proprietà commutativa dell’addizione che ci dice che invertendo l’ordine degli addendi la somma non cambia, pertanto li analizzeremo come unico caso.

La domanda, posta in italiano, consiste nel capire che numero bisogna sommare al numero 23 per ottenere come risultato 54, quindi risulta chiaro dalla proprietà vista prima (attenzione che la proprietà è letta al contrario cioè da destra a sinistra) che

   

Infatti facendo un disegno risulta chiaro

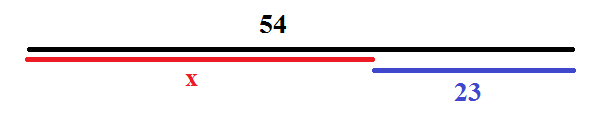
se il segmento nero (54) è uguale a quello rosso () più quello blu (23) allora il segmento rosso lo potrò ottenere facendo quello nero meno quello blu.

Caso 3

Il caso 3, cioè , utilizza esattamente la proprietà vista sopra, infatti

   

Ancora una volta un disegno è assolutamente chiarificatore

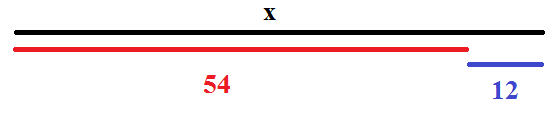
se al segmento nero () togliamo il segmento rosso (54) e quello che rimane è il segmento blu (12) allora necessariamente il segmento nero è uguale alla somma tra il segmento rosso e quello blu.

Caso 4

Vediamo infine il caso 4, ossia , e anche qui utilizziamo esattamente la proprietà vista precedentemente, infatti

   

Anche qui vediamo di spiegare il tutto attraverso un disegno

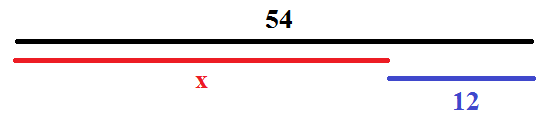
se il segmento nero (54) meno il segmento rosso () è uguale al segmento blu (12) allora necessariamente anche il segmento rosso è uguale al segmento nero meno il segmento blu.

Approfondimento sulla risoluzione di esercizi del tipo .

Dopo questa lezione vediamo di consolidare i concetti con una serie di esercizi mirati. Vai ai quiz (il quiz verrà aperto in una nuova scheda):

Quiz 1	Quiz 10
Quiz 2	Quiz 11
Quiz 3	Quiz 12
Quiz 4	Quiz 13
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9