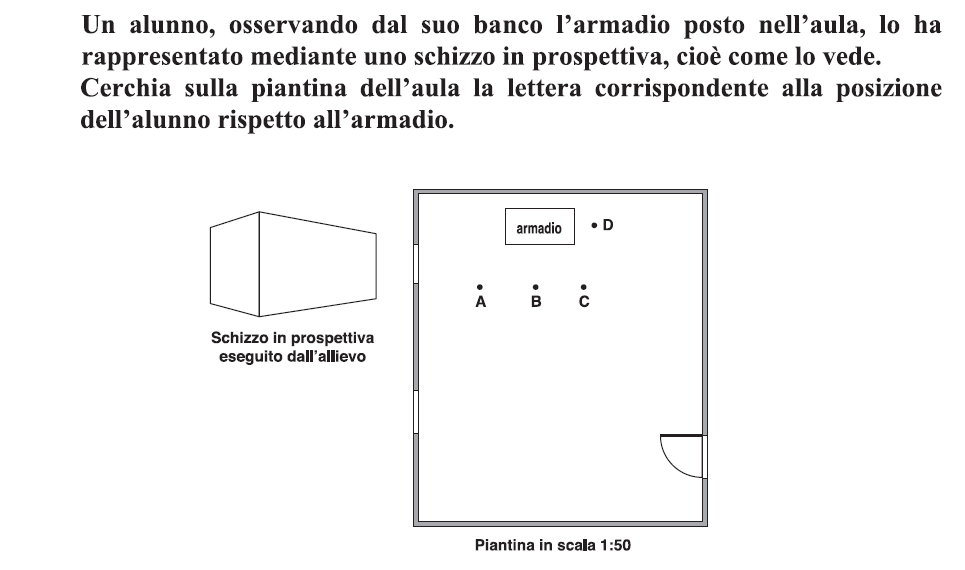
SVOLGIMENTO
Visualizza la soluzione |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |
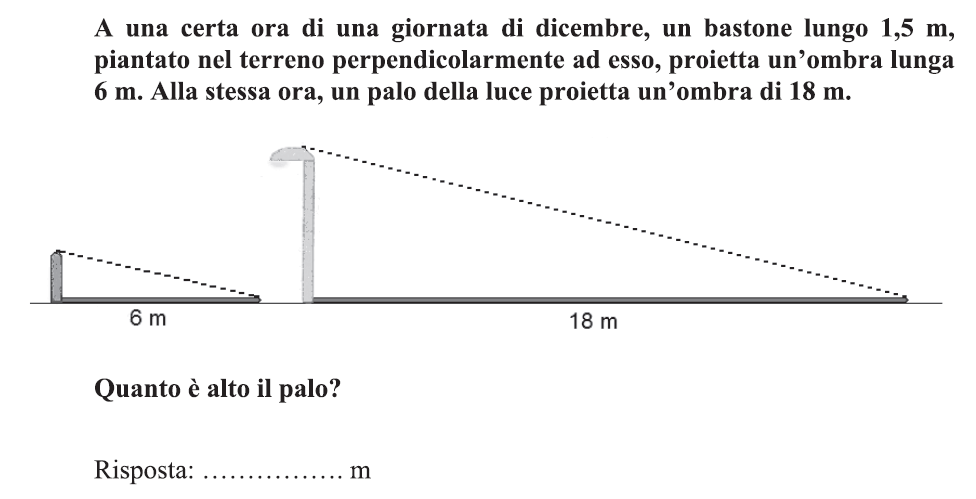
 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |
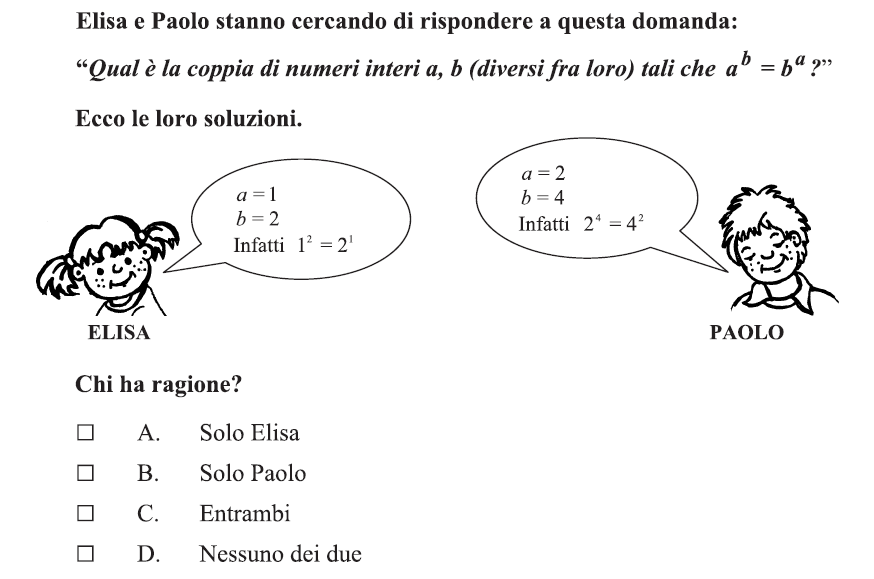
 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |

 |
TORNA ALLA PAGINA CON GLI ESERCIZI SVOLTI IN PREPARAZIONE ALLA PROVA INVALSI DI MATEMATICA |  |